1998 LS 8.1 Dichte info schwer: Unterschied zwischen den Versionen
Neh (Diskussion | Beiträge) |
Neh (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (109 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[1998 LS 8.1 Dichte| Link zur übergeordneten Seite]] | [[1998 LS 8.1 Dichte| Link zur übergeordneten Seite]] | ||
== Einleitung == | |||
Sie haben bestimmt schon gesagt oder gedacht: "Gold ist doch schwerer als Wachs". | Sie haben bestimmt schon gesagt oder gedacht: "Gold ist doch schwerer als Wachs". | ||
Dies ist jedoch nicht ganz richtig, da eine große Menge Wachs schwerer sein kann als ein kleines Stückchen Gold. Es kommt auch auf die "Menge" an, also auf das Volumen. Richtig ausgedrückt müsste man sagen: "Gold hat eine höhere Dichte als Wachs". | |||
== Dichte, das Verhältnis von Masse zu Volumen eines Körpers == | |||
Körper (z.B. Brücken) können aus unterschiedlichen Stoffen bestehen, welche unterschiedliche Dichten haben. Zum Beispiel hat Aluminium eine Dichte von 2,7 g/cm³, Kupfer von 8,96 g/cm³ und reines Gold eine Dichte von 19,3 g/cm³. | |||
<div style="border:1px solid black; padding:10px; display:inline-block;"> | |||
Die Dichte ρ (Rho) eines Körpers ist das Verhältnis von Masse zu Volumen: | Die Dichte ρ (Rho) eines Körpers ist das Verhältnis von Masse zu Volumen: | ||
<math>Dichte = \rho = \frac{m}{V} = \frac{\text{Masse}}{\text{Volumen}}</math> | <math>Dichte = \rho = \frac{m}{V} = \frac{\text{Masse}}{\text{Volumen}}</math> | ||
</div> | </div> | ||
Zum Beispiel hat Aluminium eine Dichte von 2,7 g/cm³, Kupfer von 8,96 g/cm³ und reines Gold eine Dichte von 19,3 g/cm³. | |||
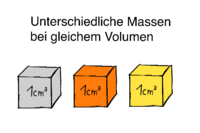
=== Unterschiedliche Masse bei gleichem Volumen === | |||
Körper (z.B. Würfel) aus unterschiedlichen Stoffen (unterschiedlichen Dichten) können also trotz gleichem Volumen unterschiedliche Massen haben. | |||
[[File:Dichte_Würfel.png|200px|rechts|mini|Würfel aus unterschiedlichen Stoffen (unterschiedliche Dichten) mit unterschiedlicher Masse aber selben Volumen]] | |||
Wenn die Dichte dreimal so hoch ist, muss die Masse auch dreimal so hoch sein, bei gleichbleibendem Volumen. | |||
<math> \text{Dichte} \uparrow = \frac{\text{Masse} \uparrow}{\text{Volumen}} </math> | |||
Eine höhere Dichte (Dichte ↑; anstelle Aluminium wird Kupfer verwendet) führt zu einer höheren Masse | |||
(Masse ↑), bei gleichbleibendem Volumen. Die beiden Seiten der Gleichung müssen ausgeglichen sein. | |||
Berechnungsbeispiel: | |||
Wenn Alumiunium (Dichte 2,7 g/cm3) durch Kupfer (Dichte 8,96 g/cm3) ersetzt wird, dann ist das Verhältnis DichteKupfer/DichteAluminium= 8,96 / 2,7 = 3,3 bei gleichbleibendem Volumen. Da beide Seiten der Gleichung ausgeglichen sein müssen, muss die Masse auch 3,3 mal höher sein, bei gleichbleibendem Volumen. | |||
=== Die Dichte in der Zahntechnik === | |||
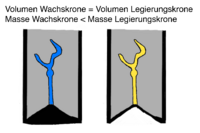
[[File:Dichte_Wachs_Gold.png|200px|rechts|mini|Das Volumen der Wachskrone ist genauso groß wie das Volumen der Legierungskrone, aber die Massen unterscheiden sich]] | |||
Schauen wir uns nun den Herstellungsprozess einer Brücke an und sehen, ob uns diese Informationen helfen: | |||
Beim Gießen von Zahnersatz (z.B. Kronen, Brücken) wird die Wachsmodellation ausgebrannt und mit einer Legierung befüllt. Das Volumen der Wachsbrücke und der Legierungsbrücke bleibt aber gleich. Sonst würde der Zahnersatz später nicht mehr auf das Modell passen. | |||
Wie bei den Würfeln wissen wir jetzt schon: Die Dichte der Legierung muss x-mal so groß sein wie die von Wachs. Obwohl beide Brücken das gleiche Volumen haben, muss die Legierungsbrücke x-mal so viel Masse haben wie die Wachsbrücke. | |||
<div style="border:1px solid black; padding:10px; display:inline-block;"> | |||
<math> Masse_{Legierungsbrücke} = x \times Masse_{Wachsbrücke} </math> | |||
</div> | |||
Dabei ist x ist das Verhältnis der Dichte der Legierung zur Dichte von Wachs. | |||
<div style="border:1px solid black; padding:10px; display:inline-block;"> | <div style="border:1px solid black; padding:10px; display:inline-block;"> | ||
<math> Masse_{ | <math> Masse_{Legierungsbrücke} = \left( \frac{Dichte_{Legierung}}{Dichte_{Wachs}} \right) \times Masse_{Wachsbrücke} </math> | ||
</div> | </div> | ||
Die Dichte der Legierung "Vielgoldium" kann der Legierungstabelle entnommen werden. | |||
Wenn wir also die Dichte von Wachs und die Masse der Wachsbrücke bestimmen, können wir die Legierungsmasse berechnen. | |||
'''Bestimmung der Dichte''' | |||
= | Die Dichte kann durch Einsetzten der Masse und des Volumens bestimmt werden. Der Wert sollte bei etwa 1 g/cm3 liegen. Die Masse von Wachs können Sie mithilfe einer Waage bestimmen. Das Volumen von Wachs bestimmen Sie mithilfe eines Messzylinders mit Wasser (ml = cm3). Die Dichte der Legierung ist in der Legierungstabelle angegeben. | ||
<div style="border:1px solid black; padding:10px; display:inline-block;"> | <div style="border:1px solid black; padding:10px; display:inline-block;"> | ||
<math>\text{ | <math> Dichte_{\text{Wachs}} = \frac{Masse_{\text{Wachsbrücke}}}{Volumen_{\text{Wachsbrücke}}} </math> | ||
</div> | </div> | ||
'''Berechnung der Legierungsmaterialkosten''' | |||
Mit bekannter Legierungsmasse können nun die erwarteten Legierungsmaterialkosten berechnet werden: | |||
<div style="border:1px solid black; padding:10px; display:inline-block;"> | <div style="border:1px solid black; padding:10px; display:inline-block;"> | ||
<math> | <math>\text{Legierungsmaterialkosten} = Masse_{\text{Legierungbrücke}} \times \text{Preis}_{\text{Legierung}}</math> | ||
</div> | </div> | ||
mit Legierungsmaterialkosten in €, Masse in g und Preis in €/g. | |||
Hinweis: Die tatsächliche Legierungsmaterialkosten erhalten wir erst nach dem Ausbetten durch Wiegen der vom Gusskanal abgetrennten Brücke. Der berechnete Wert sollte aber sehr nah dran liegen. | |||
'''Sprinterinhalte:''' | |||
Die Würfel stehen zum Versuch zur Verfügung. Probieren Sie es selbst aus. | |||
Aktuelle Version vom 27. September 2023, 17:32 Uhr
Einleitung
Sie haben bestimmt schon gesagt oder gedacht: "Gold ist doch schwerer als Wachs". Dies ist jedoch nicht ganz richtig, da eine große Menge Wachs schwerer sein kann als ein kleines Stückchen Gold. Es kommt auch auf die "Menge" an, also auf das Volumen. Richtig ausgedrückt müsste man sagen: "Gold hat eine höhere Dichte als Wachs".
Dichte, das Verhältnis von Masse zu Volumen eines Körpers
Körper (z.B. Brücken) können aus unterschiedlichen Stoffen bestehen, welche unterschiedliche Dichten haben. Zum Beispiel hat Aluminium eine Dichte von 2,7 g/cm³, Kupfer von 8,96 g/cm³ und reines Gold eine Dichte von 19,3 g/cm³.
Die Dichte ρ (Rho) eines Körpers ist das Verhältnis von Masse zu Volumen:
[math]\displaystyle{ Dichte = \rho = \frac{m}{V} = \frac{\text{Masse}}{\text{Volumen}} }[/math]
Zum Beispiel hat Aluminium eine Dichte von 2,7 g/cm³, Kupfer von 8,96 g/cm³ und reines Gold eine Dichte von 19,3 g/cm³.
Unterschiedliche Masse bei gleichem Volumen
Körper (z.B. Würfel) aus unterschiedlichen Stoffen (unterschiedlichen Dichten) können also trotz gleichem Volumen unterschiedliche Massen haben.
Wenn die Dichte dreimal so hoch ist, muss die Masse auch dreimal so hoch sein, bei gleichbleibendem Volumen.
[math]\displaystyle{ \text{Dichte} \uparrow = \frac{\text{Masse} \uparrow}{\text{Volumen}} }[/math]
Eine höhere Dichte (Dichte ↑; anstelle Aluminium wird Kupfer verwendet) führt zu einer höheren Masse (Masse ↑), bei gleichbleibendem Volumen. Die beiden Seiten der Gleichung müssen ausgeglichen sein.
Berechnungsbeispiel: Wenn Alumiunium (Dichte 2,7 g/cm3) durch Kupfer (Dichte 8,96 g/cm3) ersetzt wird, dann ist das Verhältnis DichteKupfer/DichteAluminium= 8,96 / 2,7 = 3,3 bei gleichbleibendem Volumen. Da beide Seiten der Gleichung ausgeglichen sein müssen, muss die Masse auch 3,3 mal höher sein, bei gleichbleibendem Volumen.
Die Dichte in der Zahntechnik
Schauen wir uns nun den Herstellungsprozess einer Brücke an und sehen, ob uns diese Informationen helfen: Beim Gießen von Zahnersatz (z.B. Kronen, Brücken) wird die Wachsmodellation ausgebrannt und mit einer Legierung befüllt. Das Volumen der Wachsbrücke und der Legierungsbrücke bleibt aber gleich. Sonst würde der Zahnersatz später nicht mehr auf das Modell passen.
Wie bei den Würfeln wissen wir jetzt schon: Die Dichte der Legierung muss x-mal so groß sein wie die von Wachs. Obwohl beide Brücken das gleiche Volumen haben, muss die Legierungsbrücke x-mal so viel Masse haben wie die Wachsbrücke.
[math]\displaystyle{ Masse_{Legierungsbrücke} = x \times Masse_{Wachsbrücke} }[/math]
Dabei ist x ist das Verhältnis der Dichte der Legierung zur Dichte von Wachs.
[math]\displaystyle{ Masse_{Legierungsbrücke} = \left( \frac{Dichte_{Legierung}}{Dichte_{Wachs}} \right) \times Masse_{Wachsbrücke} }[/math]
Die Dichte der Legierung "Vielgoldium" kann der Legierungstabelle entnommen werden. Wenn wir also die Dichte von Wachs und die Masse der Wachsbrücke bestimmen, können wir die Legierungsmasse berechnen.
Bestimmung der Dichte
Die Dichte kann durch Einsetzten der Masse und des Volumens bestimmt werden. Der Wert sollte bei etwa 1 g/cm3 liegen. Die Masse von Wachs können Sie mithilfe einer Waage bestimmen. Das Volumen von Wachs bestimmen Sie mithilfe eines Messzylinders mit Wasser (ml = cm3). Die Dichte der Legierung ist in der Legierungstabelle angegeben.
[math]\displaystyle{ Dichte_{\text{Wachs}} = \frac{Masse_{\text{Wachsbrücke}}}{Volumen_{\text{Wachsbrücke}}} }[/math]
Berechnung der Legierungsmaterialkosten
Mit bekannter Legierungsmasse können nun die erwarteten Legierungsmaterialkosten berechnet werden:
[math]\displaystyle{ \text{Legierungsmaterialkosten} = Masse_{\text{Legierungbrücke}} \times \text{Preis}_{\text{Legierung}} }[/math]
mit Legierungsmaterialkosten in €, Masse in g und Preis in €/g. Hinweis: Die tatsächliche Legierungsmaterialkosten erhalten wir erst nach dem Ausbetten durch Wiegen der vom Gusskanal abgetrennten Brücke. Der berechnete Wert sollte aber sehr nah dran liegen.
Sprinterinhalte:
Die Würfel stehen zum Versuch zur Verfügung. Probieren Sie es selbst aus.