WAK Material 3: Unterschied zwischen den Versionen
Neh (Diskussion | Beiträge) |
Neh (Diskussion | Beiträge) |
||
| Zeile 27: | Zeile 27: | ||
So wird sich z.B. eine Kupferstange mit einem linearen Wärmeausdehnungskoeffizienten von 16,4 · 10<sup>-6</sup> 1/K und 1,0000000 Meter länge bei einer Temperaturerhöhung um 1 Kelvin auf 1,0000164 dehnen. | So wird sich z.B. eine Kupferstange mit einem linearen Wärmeausdehnungskoeffizienten von 16,4 · 10<sup>-6</sup> 1/K und 1,0000000 Meter länge bei einer Temperaturerhöhung um 1 Kelvin auf 1,0000164 dehnen. | ||
<!-- | |||
Die Änderung der Länge (Längenausdehnung) ∆L ist gleich dem linearern Wärmeausdehnungskoeffizient α mal die Ursprungslänge (L_0) mal die Änderung der Temperatur (∆T). | Die Änderung der Länge (Längenausdehnung) ∆L ist gleich dem linearern Wärmeausdehnungskoeffizient α mal die Ursprungslänge (L_0) mal die Änderung der Temperatur (∆T). | ||
Als Formel: | Als Formel: | ||
| Zeile 34: | Zeile 34: | ||
Deshalb kann man den linearer Wärmeausdehnungskoeffizient ''α'' von Kupfer auch mit 16,4 μm/m · K angeben. | Deshalb kann man den linearer Wärmeausdehnungskoeffizient ''α'' von Kupfer auch mit 16,4 μm/m · K angeben. | ||
--> | |||
Version vom 4. März 2023, 21:16 Uhr
Wärmeausdehnungskoeffizient
Der Wärmeausdehnungskoeffizent (WAK) ist ein Materialwert, der angibt, wie stark sich ein Material bei einer Temperaturänderung ausdehnt (thermische expansion) oder zusammenzieht (thermische kontraktion). Der WAK wird üblicherweise in der Einheiten von 1/K (eins durch Kelvin) angegeben. Kelvin ist eine Maßeinheit für die Temperatur und wird in der Wissenschaft und Technik verwendet. In Bezug auf Grad Celcius (°C) sind 0 Kelvin das gleiche wie -273,15 Grad Celsius. 273,15 Kelvin sind also 0 Grad Celsius und 373,15 Kelvin somit 100 Grad Celsius.
Linearer Wärmeausdehnungskoeffizient
Festkörper expandieren (dehen sich aus) bei Erwärmung. Die Ausdehnung in eine Raumrichtung wird als linearer Wärmeausdehnungskoeffizient α oder Längenausdehnungskoeffizienten α angegeben. Der linearer Wärmeausdehnungskoeffizient α beschreibt, um den wievielten Teil seiner Länge sich ein Körper bei einer Temperaturerhöhung um 1 K verlängert.
So wird sich z.B. eine Kupferstange mit einem linearen Wärmeausdehnungskoeffizienten von 16,4 · 10-6 1/K und 1,0000000 Meter länge bei einer Temperaturerhöhung um 1 Kelvin auf 1,0000164 dehnen.
Bei den meisten Feststoffen expandieren und kontrahieren die Stoffe in alle Raumrichtungen mit dem Längenausdehnungskoeffizienten α.
Bedeutung des WAK in der Zahntechnik
Der WAK von Dentallegierungen ist in Legierungstabellen von großer Bedeutung. Deutlich wird dies bei einem Keramikbrand auf eine Aufbrennlegierung. Dabei können 3 Fälle auftreten:
1. Der WAK der Legierung ist gleich dem WAK der Keramik. WAK_Legierung = WAK_Keramik.
2. Der WAK der Legierung ist größer als der WAK der Keramik. WAK_Legierung > WAK_Keramik
3. Der WAK der Legierung ist kleiner als der WAK der Keramik. WAK_Legierung < WAK_Keramik
1. Der WAK der Legierung ist gleich dem WAK der Keramik.
Beide Stoffe dehnen sich bei Erwärmung gleich aus. Hört sich zunächst gut an, ist aber leider kaum zu erreichen, da man nie absolut gleiche WAK Werte bei zwei Stoffen erreichen kann. Die Gefahr wäre demnach sehr groß, dass bei kleinen Abweichungen in der Legierung oder der Keramik der WAK der Keramik größer ist (siehe WAK_Legierung<WAK_Keramik).
2. Der WAK der Legierung ist größer als der WAK der Keramik.
Im Aufwärmvorgang expandiert (ausdehnen) die Legierung stärker als die Keramik. Im Abkühlungsvorgang kontrahiert (zusammenziehen) die Legierung stärker als die Keramik der Verblendung. Da die Keramik an der Legierungsoberfläche gebunden ist, wird die Keramik gezwungen etwas kleiner zu werden als sie normalerweise würde. Die Keramik wird also im Grenzbereich zwischen Keramik und Metall zusammen gedrückt. Dies führt zu Druckspannungen (wird zusammen gedrückt), welche spröde Werkstoffe wie Keramiken gut aufnehmen können.
3. Der WAK der Legierung ist kleiner als der WAK der Keramik.
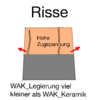
Im Aufwärmvorgang expandiert (ausdehnen) die Keramik stärker als die Legierung. Im Abkühlungsvorgang kontrahiert (zusammenziehen) demnach die Keramik auch stärker als die Legierung. Die Keramik ist mit dem Legierungsgerüst verbunden. Daher wird die Keramik von dem Legierungsgerüst gezwungen etwas größer zu bleiben als sie normalerweise würde. Die Keramik wird also im Grenzbereich zwischen Keramik und Metall auseinander gezogen. Dies führt zu Zugspannung (wird auseinander gezogen), welches für einen spröden Werkstoff wie Keramik die Rissbildung stark erhöht.
Optimaler Legierungs-WAK und der Grund für Risse und Abplatzungen in der Verblendung
Die Legierung und die Keramik müssen demnach aufeinander abgestimmt sein. Optimal ist für die Legierung ein um 0,5 bis 1 µm/m*K größeren WAK Wert. So wird die Legierung bei der Abkühlung stärker konrahieren und die Keramik (die an der Legierung haftet) wird leicht zusammengedrückt.
Ist der WAK der Legierung viel größer als der WAK der Keramik führt dies zu Abplatzungen, da die Keramik gezwungen wird, stark zu schrumpfen und somit die Druckspannung (Keramik wird zusammengedrückt) sehr hoch wird. Ist der WAK der Legierung viel kleiner als der WAK der Keramik, führt dies zu Rissen, da die Keramik gezwungen wird, sich stark auszudehnen und somit die Zugspannung (Keramik wird auseinander gezogen) sehr hoch wird.