1998 LS 8.1 Dichte info schwer
Einleitung
Um die Legierugnsmaterialkosten zu berechnen müssen Sie den Preis und die Legierungsmasse kennen. Den Preis der Legierung können Sie der Legierungstabelle entnehmen, die Masse der Legierung ist aber leider nicht bekannt.
[math]\displaystyle{ \text{Legierungsmaterialkosten} = Masse_{\text{Legierung}} \times \text{Preis}_{\text{Legierung}} }[/math]
Bevor Sie die Legierungsmaterialkosten berechnen können, sollten Sie sich zunächst über die Dichte informieren. Diese ist von Bedeutung, wenn Sie erklären wollen, was sie tun.
Dichte
Sie haben bestimmt schon gesagt oder gedacht: "Gold ist doch schwerer als Wachs".
Dies ist jedoch nicht ganz richtig, da eine große Menge Wachs schwerer sein kann als ein kleines Stückchen Gold. Es kommt auch auf die "Menge" an, bzw. auf das Volumen.
Richtig ausgedrückt müsste man sagen: "Gold hat eine höhere Dichte als Wachs". Aber warum genau?
Die Dichte ρ (Rho) eines Körpers ist das Verhältnis von Masse zu Volumen:
[math]\displaystyle{ Dichte = \rho = \frac{m}{V} = \frac{\text{Masse}}{\text{Volumen}} }[/math]
Körper aus einem bestimmten Stoff, wie z. B. eine NEM-Legierung, können eine beliebige Größe (Volumen) oder Masse besitzen, aber die Dichte eines Stoffes bleibt immer gleich.
Beispiel:
Eine kleines NEM-Inlay hat ein Gewicht von ca. 1 g und ein Volumen von ca. 0,115 cm3.
Eine großere NEM-Krone hat ein Gewicht von ca. 4 g und ein Volumen von ca. 0,46 cm3.
Vervierfacht sich das gewicht, vervierfacht sich auch das Volumen. Die Dichte der NEM-Legierung und damit das Verhältnis von Masse zu Volumen bleibt immer bei 8,7 g/cm3 und damit gleich.
Das Verhältnis von Masse zu Volumen bei einem Stoff bleibt also gleich. Erhöht sich die Masse, muss sich auch das Volumen erhöhen und umgekehrt. Die erhöhung des einen Wertes führt zu einer erhöhung eines anderen Wertes, dies nennt man Proportionalität.
Frage: Aber was, wenn wir das Volumen eines Stoffes (Wachsmodellation) mit einem anderen Stoff (Legierung) ausfüllen wollen?
Das Volumen der Wachsmodellation wird mit einer Legierung gefüllt
Beim Gießen von Zahnersatz (z.B. Kronen, Brücken, Inlays) wird die Wachsmodellation ausgebrannt und mit einer Legierung befüllt. Das Volumen des Zahnersatzes bleibt aber gleich. Sonst würde der Zahnersatz später nicht mehr auf das Modell passen.
Außer NEM werden alle Legierungen in Plättchen geliefert.
Frage: Aber wieviel Legierungsmasse brauchen wir um das Volumen aufzufüllen?
Berechnung der Legierungsmasse
Da beide Materialien (Wachs und Legierung) den gleichen Raum einnehmen (gleiches Volumen), aber die Legierung eine viel höhere Dichte hat, muss sie viel "schwerer" sein als das Wachs.
Beispiel: Angenommen die Dichte von Wachs ist 1 g/cm3 und die Dichte einer NEM-Legierung ist 8,7 g/cm3. Die Dichte der NEM-Legierung ist dann 8,7 mal zu höher als die Dichte der Wachsmodellation. Da das Volumengleich groß ist, muss die Masse auch 8,7 mal höher sein.
[math]\displaystyle{ Masse_{Legierung} = \left( \frac{\rho_{Legierung}}{\rho_{Wachs}} \right) \times m_{Wachs} }[/math]
Hinweis: Die Legierungsmasse könnte auch direkt über das Volumen der Wachsmodellation bestimmt werden, das Volumen lässt sich allerdings nicht so genau bestimmen und man müsste jedesmal umständlich das Volumen bestimmen anstelle einfach das Gewicht zu bestimmen.
Berechnung der Legierungsmaterialkosten
Mit bekannter Legierungsmasse können nun die erwarteten Legierungsmaterialkosten berechnen werden:
[math]\displaystyle{ \text{Legierungsmaterialkosten} = Masse_{\text{Legierung}} \times \text{Preis}_{\text{Legierung}} }[/math]
mit Legierungsmaterialkosten in €, Masse in g und Preis in €/g.
Hinweis: Die tatsächliche Legierungsmaterialkosten erhalten wir erst nach dem Ausbetten durch wiegen des vom Gusskanal abgetrennten Zahnersatzes. Der berechnete Wert sollte aber sehr nah dran liegen.
Messung der Masse und des Volumens bei Festkörpern
Das Volumen von Festkörpern kann bei einfachen Formen durch die ganzen Formeln berechnet werden, welche Sie im Matheunterricht kennen gelernt haben (z.B. bei Würfeln, Kugeln, Zylindern). Das Volumen von komplizierten Festkörpern (z.B. Brücken) kann man folgendermaßen bestimmen:
Messung der Masse
Die Masse wird gewogen (s. Zusammensetzung Massenanteil).
Einfache Messung des Volumens
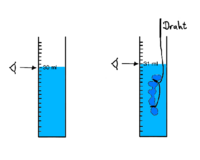
Um das Volumen eines Objekts zu bestimmen, kann man es in einen Messzylinder mit Flüssigkeit eintauchen. Man notiert das Anfangsvolumen der Flüssigkeit. Nach dem möglichst blasenfreien Eintauchen des Objekts misst man das verdrängte Volumen. Die Differenz dieser beiden Messungen gibt das Volumen des Objekts an. Beachten Sie: ml = cm3.
Volumen der Wachsmodellation = Wasserstand nach dem Eintauchen - Wasserstand vor dem Eintauchen
Hinweis: Wenn die Dichte des Objektes kleiner ist als die Dichte der Flüssigkeit schwimmt das Objekt. Dann muss man es runterdrücken.
Dichte berechnen
Die Dichte kann durch einsetzten der Masse und des Volumens bestimmt werden. Der Wert sollte in der nähe von 1 g/cm3 liegen.
[math]\displaystyle{ \rho_{\text{Wachs}} = \frac{m_{\text{Wachs}}}{V_{\text{Wachsmodellation}}} }[/math]
Anschließend müssen Sie wieder zurück zur Berechnung der Legierungsmasse und dann können Sie die Legierungsmaterialkosten berechnen.